"Entre dois números reais sempre existe um número racional".
Usaremos um pacato stick domesticado para provar esse teorema.
Colocaremos um par qualquer de números reais sobre pontos de uma reta e provaremos que entre esse par de pontos há um número racional. O stick comprovará o teorema com passadas a partir do número 
Iniciamos a nossa demonstração considerando um par de números reais 
. Convidamos o stick a se posicionar sobre o ponto da reta real (à esquerda do ponto 
).
Estendemos sobre o intervalo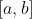 
Escolhemos um número inteiro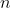 
)
Como o stick anda com passadas de tamanho fixo, existe um inteiro positivo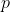 
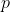
Desde que as passadas do stick são uniformes de tamanho menor do que o comprimento do tapete vermelho, ele não poderá saltar o tapete para se posicionar à direita do tapete vermelho, ou seja, existe um inteiro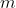 
de sorte que na 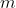-ésima passada o stick estará sobre o tapete vermelho.
Por outro lado, na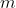 
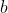
Para finalizar, vale observar que no caso 
nada precisa ser demonstrado e, no caso 
, sugiro que você escolha um stick que esteja disposto a andar no sentido negativo da reta.
Nenhum comentário:
Postar um comentário
É possível comentar utilizando a linguagem LaTeX! Vale a pena lembrar que as expressões matemáticas no LaTex devem ser escritas entre cifrões. Por exemplo, para obter $f: \mathbb{R} \rightarrow \mathbb{R}$, você deve escrever f: \mathbb{R} \rightarrow \mathbb{R} entre cifrões.